


This webpage describes my research in a detailed manner until 2007. For a description of my recent results since then, and a list of publications, see here.
Ages ago, I started my career in the Department of Mathematics at the University of Caen. My interests then gradually shifted from "pure" number theory to computational number theory and related problems in cryptography, most notably integer factorization and lattice reduction. In this area, I obtained average-case bounds for the celebrated LLL algorithms and once held the world record for the best proven bound on the complexity of integer factorization. Currently the core of my work deals with analysis of algorithms. I am especially interested in applications of dynamical systems theory to some of the major algorithms and data structures studied by theoretical computer scientists. I feel for instance responsible for the introduction of transfer operators in this area. My most recent contributions deal with the average-case analysis of lattice reduction in two or more dimensions, the exact analysis of a rich class of continued fraction algorithms, the application of transfer operators to analytic information theory, and the related analysis of digital trees ("tries") under nonuniform input models.
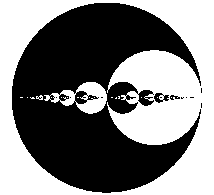


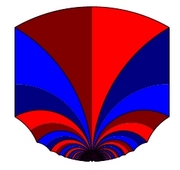
The Gaussian algorithm for lattice reduction in dimension 2 is precisely analysed under a class of realistic probabilistic models, which are of interest when applying the Gauss algorithm "inside" the LLL algorithm. The proofs deal with the underlying dynamical systems and transfer operators. All the main parameters are studied: execution parameters which describe the behaviour of the algorithm itself as well as output parameters, which describe the geometry of reduced bases.


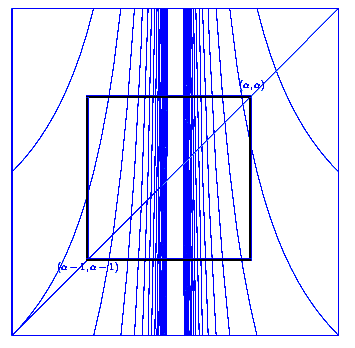
This paper considers numeration schemes, defined in terms of dynamical systems and studies the set of reals which obey some constraints on their digits. Classically, the studied constraints involve each digit in an independent way. Here, more conditions are studied, which only provide (additive) constraints on each digit prefix. The main example of interest deals with reals whose all the digit prefix averages in their continued fraction expansion are bounded by M. We first provide a characterization of the Hausdorff dimension , in terms of the dominant eigenvalue of the weighted transfer operator relative to the dynamical system. We then come back to our main example; with the previous characterization at hand and use of the Mellin Transform, we exhibit the behaviour of |s_M-1| when the bound $M$ becomes large.
In pattern matching algorithms, two characteristic parameters play an important rôle : the number of occurrences of a given pattern, and the number of positions where a pattern occurrence ends. These two parameters may differ in a significant way. Here, we consider a general framework where the text is produced by a probabilistic source, which can be built by a dynamical system. Such ``dynamical sources'' encompass the classical sources --memoryless sources, and Markov chains--, and may possess a high degree of correlations. We are mainly interested in two situations : the pattern is a general word of a regular expression, and we study the number of occurrence positions -- the pattern is a finite set of strings, and we study the number of occurrences. In both cases, we determine the mean and the variance of the parameter, and prove that its distribution is asymptotically Gaussian. In this way, we extend methods and results which have been already obtained for classical sources to this general ``dynamical'' framework. Our methods use various techniques: formal languages, and generating functions, as in previous works. However, in this correlated model, it is not possible to use a direct transfer into generating functions, and we mainly deal with generating operators which generate... generating functions.
We provide sharp estimates for the probabilistic behaviour of the main parameters of the Euclid algorithm, and we study in particular the distribution of the bit-complexity which involves two main parameters : digit-costs and length of continuants. We perform a "dynamical analysis" which heavily uses the dynamical system underlying the Euclidean algorithm. Baladi and Vall'ee [2] have recently designed a general framework for "distributional dynamical analysis", where they have exhibited asymptotic gaussian laws for a large class of digit-costs. However, this family contains neither the bit-complexity cost nor the length of continuants. We first show here that an asymptotic gaussian law also holds for the length of continuants at a fraction of the execution. There exist two gcd algorithms, the standard one which only computes the gcd, and the extended one which also computes the Bezout pair, and is widely used for computing modular inverses. The extended algorithm is more regular than the standard one, and this explains that our results are more precise for the extended algorithm. We prove that the bit-complexity of the extended Euclid algorithm asymptotically follows a gaussian law, and we exhibit the speed of convergence towards the normal law. We describe also conjectures [quite plausible], under which we can obtain an asymptotic gaussian law for the plain bit-complexity, or a sharper estimate of the speed of convergence towards the gaussian law.
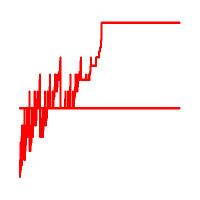
We solve a problem by V. I. Arnold dealing with "how random" modular arithmetic progressions can be. After making precise how Arnold proposes to measure the randomness of a modular sequence, we show that this measure of randomness takes a simplified form in the case of arithmetic progressions. This simplified expression is then estimated using the methodology of dynamical analysis, which operates with tools coming from dynamical systems theory. In conclusion, this study shows that modular arithmetic progressions are far from behaving like purely random sequences, according to Arnold's definition.
Here's the big chart of what is going on as regards dynamical analysis of Euclidean algorithms. This big survey paper combines methods from dynamical system theory and analytic combinatorics and serves as lecture notes for a short course I gave in 2004 at CIRM, Luminy. Six types of algorithms (including those based on least significant digits, most significant digits, odd and even remainders, subtractions, and so on) are cast into a unifying framework. Statistics on digits and number of iterations (as well as many other cost measures) can be thoroughly analysed. [PS]
These are slides relative to a general analysis of occurrences of patterns in texts produced by all sorts of sources. Presented at the Indo-French Workshop in Computer Science, Bangalore, February 2006 :-).





Keywords: Dynamical systems, Transfer operator, Hausdorff dimension,
Quasi-Powers Theorem, Large deviations,
Shifting of the mean, Mellin transform analysis.
Real Numbers with
Bounded Digit Averages. Here is the shorter version
(everything is relative!) which appeared in the Third Colloquium on
Combinatorics, Probability, Trees, and Algorithms
[or a permutation thereof], Vienna, September 2004.







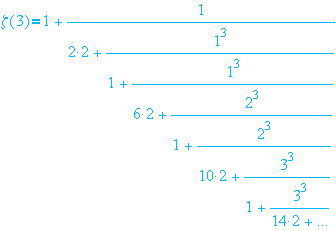




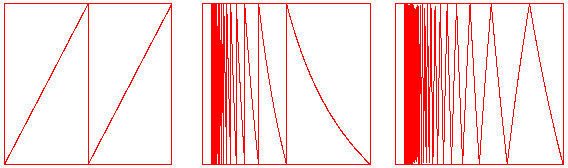

 Back to my Home Page.
Back to my Home Page.